이진 트리
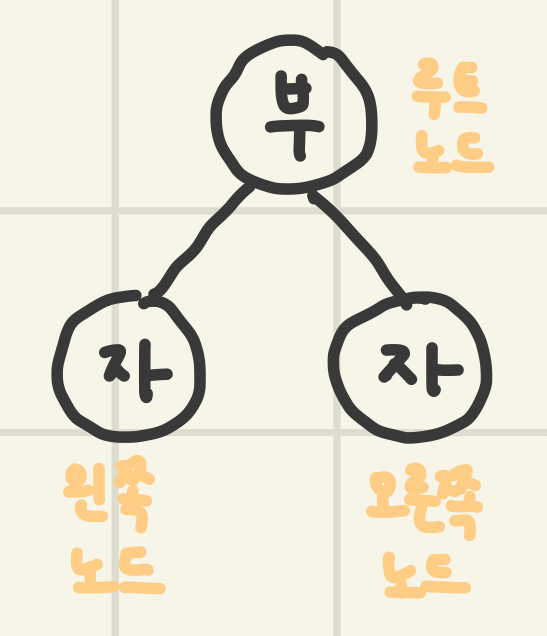
이진 트리는 부모인 루트 노드와, 자식인 왼쪽 노드 + 오른쪽 노드를 가지는 것이 기본 모양이다.
DFS
DFS(Depth-First Search)는 깊이 우선 탐색으로, 루트 노드(혹은 다른 임의의 노드)에서 시작해 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법이다.
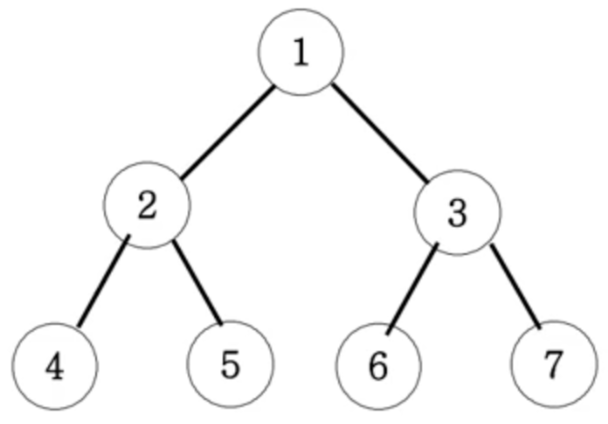
- 전위 순회 출력 (부모-왼쪽-오른쪽) : 1 - 2 - 4 - 5 - 3 - 6 - 7
- 중위 순회 출력 (왼쪽-부모-오른쪽) : 4 - 2 - 5 - 1 - 6 - 3 - 7
- 후위 순회 출력 (왼쪽-오른쪽-부모) : 4 - 5 - 2 - 6 - 7 - 3 - 1
DFS의 구현
class Node {
int data;
Node lt, rt;
public Node(int val) {
data=val;
lt=rt=null;
}
}
public class Main {
Node root;
public void DFS(Node root) {
if(root == null) return;
else {
System.out.print(root.date + " "); // 전위순회
DFS(root.lt);
System.out.print(root.date + " "); // 중위순회
DFS(root.rt);
System.out.print(root.date + " "); // 후위순회
}
}
public static void main(String arg[]) {
Main tree = new Main();
tree.root = new Node(1);
tree.root.lt = new Node(2);
tree.root.rt = new Node(3);
tree.root.lt.lt = new Node(4);
tree.root.lt.rt = new Node(5);
tree.root.rt.lt = new Node(6);
tree.root.rt.rt = new Node(7);
tree.DFS(tree.root)
}
}
활용 문제
부분집합 구하기
class Subset {
static int n;
static boolean[] visited;
public void DFS(int l) {
if(l == n+1) {
String tmp = "";
for(int i=1; i<=n; i++) {
if(visited[i]) tmp += (i + " ");
}
// 공집합이 아닌 경우에만 출력
if(tmp.length() > 0) System.out.println(tmp);
} else {
// 추가하는 경우
visited[l] = true;
DFS(l+1);
// 추가하지 않는 경우
visited[l] = false;
DFS(l+1);
}
}
public static void main(String[] args) {
Main T = new Main();
n = 3;
visited = new boolean[n+1];
T.DFS(1);
}
}
조합 구하기
- 관련 문제 : [프로그래머스] 구슬을 나누는 경우
/**
* n개 중에 r개 뽑기
*/
class Combination {
public int solution(int n, int r) {
return dfs(n, r);
}
public int dfs(int n, int r) {
if (n == r || r == 0) {
return 1;
} else {
return dfs(n - 1, r - 1) + dfs(n - 1, r);
}
}
}
💻 메모이제이션 활용
class Combination {
private int[][] memo;
public int solution(int n, int r) {
memo = new int[n + 1][r + 1];
return dfs(n, r);
}
public int dfs(int n, int r) {
if (memo[n][r] > 0) {
return memo[n][r];
}
if (n == r || r == 0) {
return 1;
} else {
return memo[n][r] = dfs(n - 1, r - 1) + dfs(n - 1, r);
}
}
}
Reference
[인프런] 자바 알고리즘 문제풀이 입문 - 부분집합 구하기(DFS)
[인프런] 자바 알고리즘 문제풀이 입문 - 조합수(메모이제이션)
'💻 Computer Science > 알고리즘' 카테고리의 다른 글
| 재귀함수 (Recursive Function) (0) | 2023.07.06 |
|---|---|
| [프로그래머스] 없는 숫자 더하기 (Java) (0) | 2022.08.27 |
| LRU (Least Recently Used) (0) | 2022.05.04 |
| 투 포인터 (two pointers) (0) | 2022.04.21 |
| [프로그래머스] n^2 배열 자르기 (Java) (0) | 2022.04.18 |
| [Algorithm] SW Expert Academy (달팽이 숫자) (0) | 2022.02.07 |
이진 트리
이진 트리는 부모인 루트 노드와, 자식인 왼쪽 노드 + 오른쪽 노드를 가지는 것이 기본 모양이다.

DFS
DFS(Depth-First Search)는 깊이 우선 탐색으로, 루트 노드(혹은 다른 임의의 노드)에서 시작해 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법이다.

- 전위 순회 출력 (부모-왼쪽-오른쪽) : 1 - 2 - 4 - 5 - 3 - 6 - 7
- 중위 순회 출력 (왼쪽-부모-오른쪽) : 4 - 2 - 5 - 1 - 6 - 3 - 7
- 후위 순회 출력 (왼쪽-오른쪽-부모) : 4 - 5 - 2 - 6 - 7 - 3 - 1
DFS의 구현
class Node {
int data;
Node lt, rt;
public Node(int val) {
data=val;
lt=rt=null;
}
}
public class Main {
Node root;
public void DFS(Node root) {
if(root == null) return;
else {
System.out.print(root.date + " "); // 전위순회
DFS(root.lt);
System.out.print(root.date + " "); // 중위순회
DFS(root.rt);
System.out.print(root.date + " "); // 후위순회
}
}
public static void main(String arg[]) {
Main tree = new Main();
tree.root = new Node(1);
tree.root.lt = new Node(2);
tree.root.rt = new Node(3);
tree.root.lt.lt = new Node(4);
tree.root.lt.rt = new Node(5);
tree.root.rt.lt = new Node(6);
tree.root.rt.rt = new Node(7);
tree.DFS(tree.root)
}
}
활용 문제
부분집합 구하기
class Subset {
static int n;
static boolean[] visited;
public void DFS(int l) {
if(l == n+1) {
String tmp = "";
for(int i=1; i<=n; i++) {
if(visited[i]) tmp += (i + " ");
}
// 공집합이 아닌 경우에만 출력
if(tmp.length() > 0) System.out.println(tmp);
} else {
// 추가하는 경우
visited[l] = true;
DFS(l+1);
// 추가하지 않는 경우
visited[l] = false;
DFS(l+1);
}
}
public static void main(String[] args) {
Main T = new Main();
n = 3;
visited = new boolean[n+1];
T.DFS(1);
}
}
조합 구하기
- 관련 문제 : [프로그래머스] 구슬을 나누는 경우
/**
* n개 중에 r개 뽑기
*/
class Combination {
public int solution(int n, int r) {
return dfs(n, r);
}
public int dfs(int n, int r) {
if (n == r || r == 0) {
return 1;
} else {
return dfs(n - 1, r - 1) + dfs(n - 1, r);
}
}
}
💻 메모이제이션 활용
class Combination {
private int[][] memo;
public int solution(int n, int r) {
memo = new int[n + 1][r + 1];
return dfs(n, r);
}
public int dfs(int n, int r) {
if (memo[n][r] > 0) {
return memo[n][r];
}
if (n == r || r == 0) {
return 1;
} else {
return memo[n][r] = dfs(n - 1, r - 1) + dfs(n - 1, r);
}
}
}
Reference
[인프런] 자바 알고리즘 문제풀이 입문 - 부분집합 구하기(DFS)
[인프런] 자바 알고리즘 문제풀이 입문 - 조합수(메모이제이션)
'💻 Computer Science > 알고리즘' 카테고리의 다른 글
| 재귀함수 (Recursive Function) (0) | 2023.07.06 |
|---|---|
| [프로그래머스] 없는 숫자 더하기 (Java) (0) | 2022.08.27 |
| LRU (Least Recently Used) (0) | 2022.05.04 |
| 투 포인터 (two pointers) (0) | 2022.04.21 |
| [프로그래머스] n^2 배열 자르기 (Java) (0) | 2022.04.18 |
| [Algorithm] SW Expert Academy (달팽이 숫자) (0) | 2022.02.07 |
