트리
트리(Tree)란?
트리는 부모노드와 자식노드로 이루어진 계층적인 구조를가지며, 무방향 그래프의 일종이자 사이클이 없는 자료구조이다.
트리는 정점(Vertex)과 간선(Edge)으로 이루어진 그래프의 일종이다. (그래프 > 트리)
트리의 용어
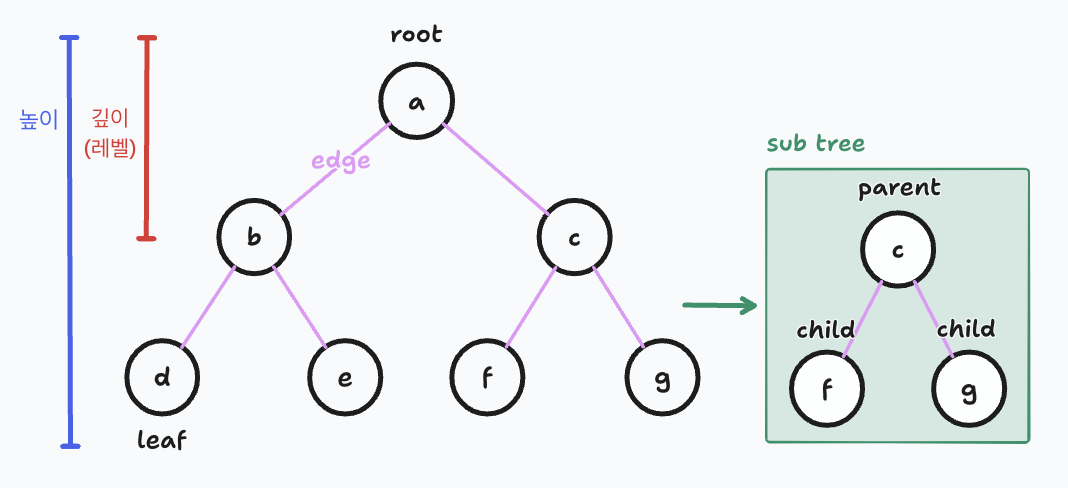
- 노드(node) : 트리를 구성하는 정점. ex) a,b,c,d,e,f,g
- 간선(edge,link) : 각 노드간 연결하는 선
- 루트 노드(root node) : 트리의 최상위 노드. 트리는 하나의 루트 노드만을 가진다. ex) a
- 리프 노드(leaf node) : 트리의 최하위 노드. ex) d,e,f,g
- 내부 노드(internal node) : 최소 1개 이상의 하위 노드를 갖는 노드. ex) a,b,c
- 부모 노드(parent node) : 하위 트리를 가지는 노드. ex) b,c의 부모 노드는 a, d,e의 부모 노드는 b, f,g의 부모 노드는 c이다.
- 자식 노드(child node) : 상위 트리를 가진 노드. ex) a의 자식 노드는 b,c, b의 자식 노드는 d,fe, c의 자식 노드는 f,g이다.
- 형제 노드(sibling node) : 같은 부모를 가지는 노드. ex) d-e, f-g, b-c는 형제노드이다.
- 조상 노드(ancestor node) : 특정 노드의 모든 부모 노드. ex) f의 조상 노드는 c,a이다.
- 서브 트리(sub tree) : 트리 내의 하위 집합. 하나의 트리는 여러 개의 서브 트리로 구성될 수 있다.
- 높이(height) : 루트 노드로부터 리프 노드까지의 거리 중 가장 긴 거리. ex) 위 트리의 높이는 2이다.
- 깊이(레벨) : 루트 노드에서 특정 노드까지 최단거리로 갔을 때의 거리. 각각의 노드마다 깊이가 다르다. ex) b노드의 깊이는 1, e노드의 깊이는 2이다.
- 크기(size) : 트리의 모든 노드의 개수. ex) 위 트리의 크기는 7이다.
- 차수(degree) : 노드의 하위 트리 개수. 즉, 연결된 자식 노드의 수를 말한다. ex) c의 차수는 2이다.
트리의 특징
1) 부모, 자식 계층 구조를 가진다.
같은 경로 상에서 어떠한 노드보다 위에 있으면 부모, 아래에 있으면 자식노드가 된다.
모든 자식 노드는 하나의 부모 노드를 갖는다.
2) V(Vertex) - 1 = E(Edge)
노드가 n개인 트리는 항상 n-1개의 간선을 가진다.
위 그림을 보면 7개의 노드가 존재하며, 간선의 수는 7 - 1 = 6개인 것을 확인할 수 있다.
3) 임의 두 노드 사이의 경로는 유일무이하게 존재한다.
트리 내 임의의 두 노드 사이의 경로는 무조건 존재한다. 어떠한 노드라도 또 다른 노드까지 가는 방법은 반드시 하나의 경로가 존재한다.
이진 트리
이진 트리(Binary Tree)란?
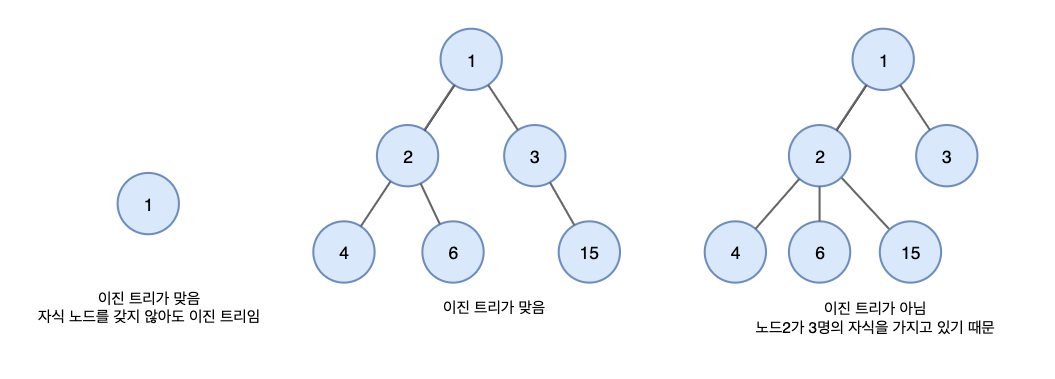
이진 트리란 각 노드의 자식 노드 수가 2개 이하로 구성되어 있는 트리를 의미한다.
이진 트리의 종류
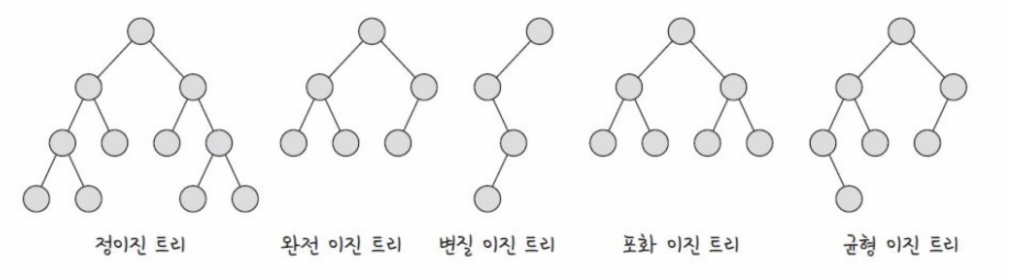
- 정이진 트리(full binary tree) : 자식 노드가 0 또는 2개인 이진 트리
- 완전이진 트리(complete binary tree) : 왼쪽에서부터 채워져 있는 이진 트리, 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있으며 마지막 레벨의 경우 왼쪽부터 채워진다.
- 변질이진 트리(degenerate binary tree) : 자식 노드가 하나밖에 없는 이진 트리
- 포화이진 트리(perfect binary tree) : 모든 노드가 꽉 차 있는 이진 트리
- ⭐️ 균형이진 트리(balanced binary tree) : 모든 노드의 왼쪽 하위 트리와 오른쪽 하위 트리의 깊이 차이가 1 이하인 트리, map과 set을 구성하는 레드블랙트리는 균형이진트리 중 하나이다.
이진 탐색 트리(Binary Search Tree)란?
이진 탐색 트리은 이진 트리의 일종이다.
노드의 왼쪽 하위 트리에는 '노드보다 작은 값', 오른쪽 하위 트리에는 '노드보다 큰 값'을 가진다는 특징을 지닌 이진 트리를 이진 탐색 트리라고 한다.
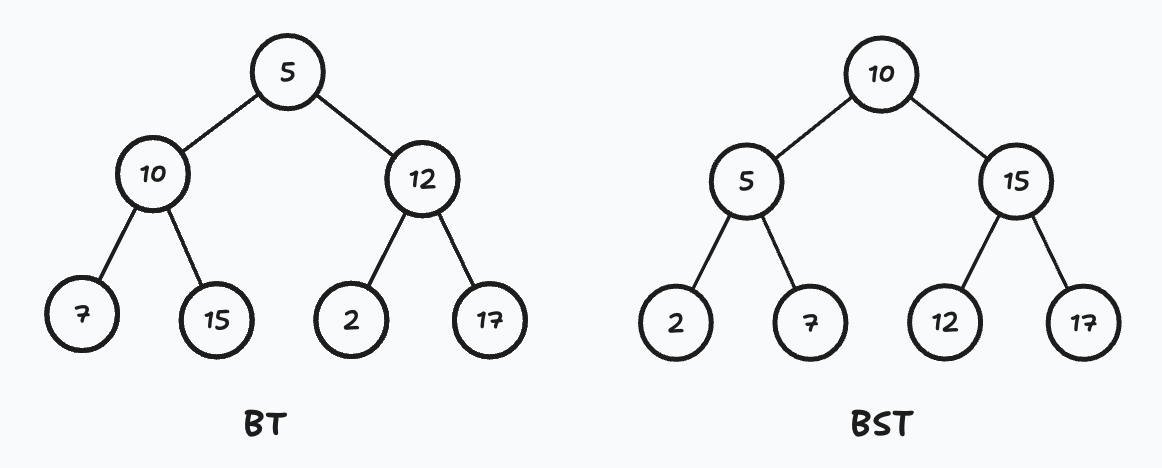
이진탐색 트리는 왼쪽에는 작은 값, 오른쪽에는 큰 값이라는 특징 때문에 검색에 매우 유용하다는 장점이 있다.
예를 들어 2 노드를 찾으려고 한다면, 굳이 전체 탐색을 하지 않고 10 노드의 왼쪽 노드들만 탐색하면 되기 때문이다.
이진탐색 트리의 시간복잡도는 O(logn)이다. 정확히 말하자면 트리의 높이에 따라 영향을 받아 O(h)이다.
하지만 이진탐색 트리는 삽입 순서에 따라 선형적인 자료구조가 될 수 있으며, 그럴 경우 worst case로 성능에 영향을 미치고 시간 복잡도가 O(n)이 된다.
이를 개선하기 위해 균형 잡히게 만든 AVL 트리와 레드블랙 트리가 등장했다.
Map이라는 자료구조는 시간복잡도가 O(logN)임을 보장받는데 그 이유는 균형 잡힌 트리인 레드블랙 트리를 기반으로 구현되어 있기 때문이다.
레드 블랙 트리에 대해서는 추후 공부 후 포스팅할 예정이다.
Referecne
https://yoongrammer.tistory.com/71
